TEORIA DE
GRAFOS
El nacimiento del concepto GRAFOS se puede situar, por
el año 1730, cuando Euler (matemático) se convirtió en el padre de la Teoría de
Grafos al modelar un famoso problema no resuelto, llamado el "problema de
los puentes de Königsberg".
Grafo
Un grafo es una pareja G = (V, A), donde V es un
conjunto de puntos, llamados vértices, y A es un conjunto de pares de vértices,
llamadas aristas. En teoría de grafos, sólo queda lo esencial del dibujo: la
forma de las aristas no son relevantes, sólo importa a qué vértices están
unidas. La posición de los vértices tampoco importa, y se puede variar para
obtener un grafo más claro.
Generalmente, se considera que colocar los
vértices en forma de polígono regular da grafos muy legibles. Prácticamente
cualquier red puede ser modelada con un grafo: una red de carreteras que
conecta ciudades, una red eléctrica o un alcantarillado.
Grafos
conexos y no conexos
Grafo conexo. En matemáticas y ciencias de la
computación es aquel grafo que entre cualquier par de sus vértices existe un
Camino (Grafo) que los une.
Algunos
grafos particulares
COMPLETO
Un grafo no dirigido G= es COMPLETO si existe
arista entre todo par de vértices de V. Sea n=|V|, el número de aristas de un
grafo completo no dirigido es exactamente |E|=n. (n-1)/2. Si se trata de un
grafo dirigido entonces |E|=n. (n-1).
Aristas
dirigidas y no dirigidas
En algunos casos es necesario asignar un sentido
a las aristas, por ejemplo, si se quiere representar la red de las calles de
una ciudad con sus inevitables direcciones únicas. El conjunto de aristas será
ahora un subconjunto de todos los posibles pares ordenados de vértices, con (a,
b) ≠ (b, a). Los grafos que contienen aristas dirigidas se denominan grafos
orientados, como el siguiente: Las aristas no orientadas se consideran
bidireccionales para efectos prácticos (equivale a decir que existen dos
aristas orientadas entre los nodos, cada una en un sentido). Se considera la
característica de "grado" (positivo o negativo) de un vértice, como
la cantidad de aristas que llegan o salen de él; para el caso de grafos no
orientados, el grado de un vértice es simplemente la cantidad de aristas que
tocan este vértice. Por ejemplo, el grado positivo (salidas) de d es 3,
mientras que el grado negativo (llegadas) de b es 1.
Grafos de
Euler
Camino de
Euler
Se dice que un grafo no dirigido G= es EULERIANO si
existe un camino cerrado, propio, simple (no se repiten aristas) pero no
necesariamente elemental que incluye todas las aristas de G. Los siguientes
lemas permiten determinar si un grafo dado es euleariano: Lema 1: Un grafo no
dirigido y conexo es euleriano si y sólo si el grado de todo vértice es par.
Lema 2: Un grafo dirigido y fuertemente conexo es euleriano si y sólo si el
grado de todo vértice es cero. Averiguar si un grafo no dirigido y conexo es
euleriano tiene un coste de θ(n), si se supone conocido el grado de cada
vértice; gracias al lema 1 basta con recorrer el conjunto de vértices y
comprobar si el grado de cada uno de ellos es par o no lo es.
ejemplo de un grafo de camino de Euler.
Ciclo o
circuito de Euler
Es un camino de Euler con la diferencia que empieza y
termina en el mismo vértice es decir es un camino cerrado que recorre
cada arista exactamente una vez. El problema de encontrar dichos caminos fue
discutido por primera vez por Leonard Euler.
Grafos Hamiltonianos.
Definición: Un
circuito o ciclo hamiltoniano es un ciclo simple que contiene todos los
vértices de G. Un circuito hamiltoniano es una trayectoria que empieza y
termina en el mismo vértice y pasa por cada vértice una sola vez.
Matriz de
adyacencia
Matriz de adyacencia. Matriz
cuadrada de orden "NxN"
Ejercicio 1:
En un torneo Nieve venció a los Faisanes una vez, el Rascacielos venció a la Tuna una vez, el Nieve venció al Rascacielos dos veces, los Faisanes vencieron a la tuna una vez y los Faisanes vencieron a Rascacielos una vez. En los ejercicios 1 al 4 use una gráfica para modelar el torneo, los equipos son los vértices. Describa el tipo de grafica usada.
1) Hay una arista entre los equipos si los equipos jugaron.
2) Hay una arista entre los equipos si los equipos para cada juego jugado.
3) Hay una arista del equipo t al equipo j si t venció a j al menos una vez.
4) Hay una arista del equipo t al equipo j para cada victoria de t sobre j.
Respuestas:
1
2
3
4
Ejercicio 2:
Determine el circuito de Euler en el siguiente grafo:
Respuesta:
(f,c)
(f,c,a)
(f,c,a,b)
(f,c,a,b,d)
(f,c,a,b,d,e)
(f,c,a,b,d,e,b)
(f,c,a,b,d,e,b,c)
(f,c,a,b,d,e,b,c,e)
(f,c,a,b,d,e,b,c,e,f)
Ejercicio 3:
Determinar el circuito de Hamilton del siguiente grafo.
Circuito de Hamilton (d,g,c,a,b,e,i,j,h,f,d)
Ejercicio 4:
Del siguiente grafo determinar:
1 ¿Tiene un camino de Euler?
2 ¿Tiene un circuito de Euler?
3 ¿Tiene circuito de Hamilton?
4 Obtener:
a) El conjunto de vértices.
b) El conjunto de aristas.
c) El conjunto de lazos.
d) El conjunto de lados paralelos.
5 Obtener la matriz adyacente.
1.- No tiene camino de Euler porque para poderlo desarrollar, se necesita que sus vértices terminen en valencia impar.
2.- No tiene circuito de Euler porque para poderlo desarrollar se necesita que todos sus vértices terminen en valencia par.
3.- No tiene circuito de Hamilton porque no cumple teorema de Dirac.
4.-
a) V={1,2,3,4,5,6,7,8,9,10}
b) E={a,b,c,d,e,f,g,h,i,j,k,l,m,n,ñ,o,p,q}
c) L={f,p}
d) LP={e,q}
5.-
ejemplo de un grafo de camino de Euler.
En un torneo Nieve venció a los Faisanes una vez, el Rascacielos venció a la Tuna una vez, el Nieve venció al Rascacielos dos veces, los Faisanes vencieron a la tuna una vez y los Faisanes vencieron a Rascacielos una vez. En los ejercicios 1 al 4 use una gráfica para modelar el torneo, los equipos son los vértices. Describa el tipo de grafica usada.
1) Hay una arista entre los equipos si los equipos jugaron.
2) Hay una arista entre los equipos si los equipos para cada juego jugado.
3) Hay una arista del equipo t al equipo j si t venció a j al menos una vez.
4) Hay una arista del equipo t al equipo j para cada victoria de t sobre j.
Respuestas:
1
2
3
4
Ejercicio 2:
Determine el circuito de Euler en el siguiente grafo:
Respuesta:
(f,c)
(f,c,a)
(f,c,a,b)
(f,c,a,b,d)
(f,c,a,b,d,e)
(f,c,a,b,d,e,b)
(f,c,a,b,d,e,b,c)
(f,c,a,b,d,e,b,c,e)
(f,c,a,b,d,e,b,c,e,f)
Ejercicio 3:
Circuito de Hamilton (d,g,c,a,b,e,i,j,h,f,d)
Ejercicio 4:
Del siguiente grafo determinar:1 ¿Tiene un camino de Euler?
2 ¿Tiene un circuito de Euler?
3 ¿Tiene circuito de Hamilton?
4 Obtener:
a) El conjunto de vértices.
b) El conjunto de aristas.
c) El conjunto de lazos.
d) El conjunto de lados paralelos.
5 Obtener la matriz adyacente.
1.- No tiene camino de Euler porque para poderlo desarrollar, se necesita que sus vértices terminen en valencia impar.
2.- No tiene circuito de Euler porque para poderlo desarrollar se necesita que todos sus vértices terminen en valencia par.
3.- No tiene circuito de Hamilton porque no cumple teorema de Dirac.
4.-
a) V={1,2,3,4,5,6,7,8,9,10}
b) E={a,b,c,d,e,f,g,h,i,j,k,l,m,n,ñ,o,p,q}
c) L={f,p}
d) LP={e,q}
5.-



















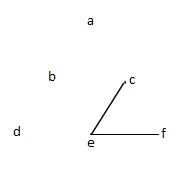





No hay comentarios:
Publicar un comentario